Objetivo Particular del Periodo:
El alumno entenderá los conceptos
elementales del álgebra lineal y los aplicará en problemas del ámbito económico
y de gestión de negocios.
4.1 Sistemas de ecuaciones lineales.
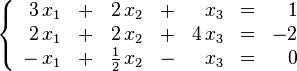
4.1 Sistemas de ecuaciones lineales.
4.1.1 Definición
En matemáticas y álgebra lineal, un sistema de ecuaciones lineales, también conocido como sistema lineal de ecuaciones o simplemente sistema lineal, es un conjunto deecuaciones lineales (es decir, un sistema de ecuaciones en donde cada ecuación es de primer grado), definidas sobre un cuerpo o un anillo conmutativo. Un ejemplo de sistema lineal de ecuaciones sería el siguiente:
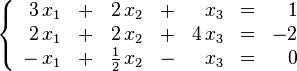
4.1.2
Sistemas de ecuaciones lineales: consistentes, inconsistentes, y su
representación paramétrica del conjunto solución.
Sistemas inconsistentes
Esta Sección se enfocará en las últimas dos situaciones: sistemas que no tienen soluciones o sistemas con una cantidad infinita de soluciones.
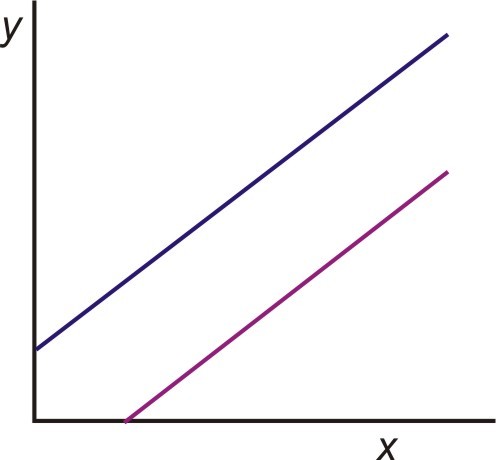
Un sistema con rectas paralelas no tendrá soluciones .
Recuerda que las rectas paralelas tienen la misma pendiente. Cuando sean graficadas, las rectas tendrán la misma inclinación con diferentes interceptos en y− Por lo tanto, las rectas paralelas nunca se intersecarán, así que no tendrán solución.

Sistemas consistentes
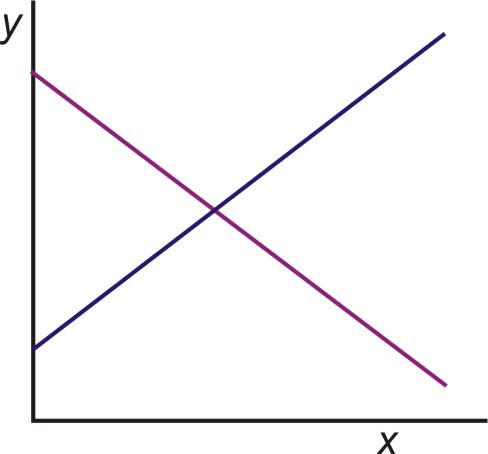
Los sistemas consistentes, por otro lado, tienen al menos una solución. Esto significa que las rectas se intersectan al menos una vez. Existen tres casos de sistemas consistentes:
- Una intersección, como generalmente se hace en las Secciones de sistemas lineales.
- Dos o más intersecciones, como se puede ver cuando una ecuación de segundo grado interseca una ecuación lineal.
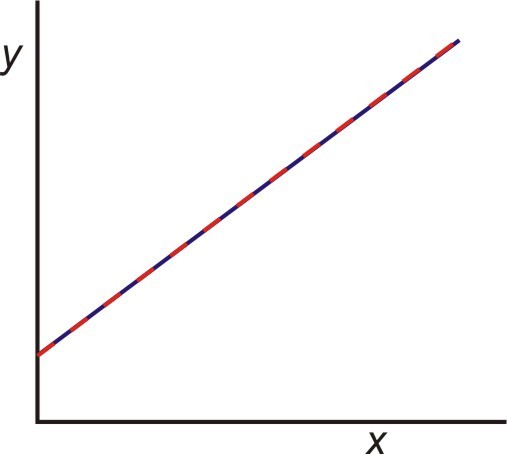
- Muchas intersecciones infinitas, como ocurre con las rectas coincidentes.


https://www.youtube.com/watch?v=k4JQQJdmmoA
matemprepa. (2014). Álgebra Intermedia - Lección 61 - B (sistemas consistentes, inconsistentes y dependientes). 19 de noviembre del 2015, de youtube.com Sitio web: https://www.youtube.com/watch?v=k4JQQJdmmoA
4.1.3 Métodos para resolución
de sistemas de ecuaciones lineales: método gráfico, igualación, sustitución,
eliminación (sumas y restas).
Método de sustitución
Es aconsejable en sistemas en los que aparecen coeficienteso
.
- Despejamos la
de la primera ecuación:
- Sustituimos en la otra ecuaciñon:
- Resolvemos la ecuacón resultante:
- Para averiguar el valor de
sustituimos el valor de
en la expresión obtenida el el paso 1
- Despejamos la
Método de igualación
- Despejamos la misma variable de ambas ecuaciones
- Igualamos las dos expresiones anteriores
- Resolvemos la ecuación resultante
- Para calcular el valor de x sustituimos
en cualquiera de las expresiones obtenidas en el paso 1
- Despejamos la misma variable de ambas ecuaciones
Método de reducción
Combinación lineal de ecuaciones : se multiplica una ecuación por ún número, la otra por otro número y se suman. La ecuación resultante de una combinación lineal es equivalente a las ecuaciones originales del sistema.
El método de reducción consiste en eliminar una incognita del sistema.- Vamos a eliminar la
. Para ello multiplico la ecuación de arriba por 3 y la de abajo por 2:
- Sumando ambas ecuaciones desapacen las x y nos queda
- Vamos a eliminar la
Algebra elemental. (2008). Sistemas de ecuaciones lineales con dos incógnitas.Métodos de resolución. 19 de noviembre del 2015, de Matemáticas, Sistemas de ecuaciones algebraicos. Sitio web: https://bitacoraed.wordpress.com/2008/03/28/sistemas-de-ecuaciones-lineales-con-dos-incognitasmetodos-de-resolucion/
4.1.4 Sistemas de ecuaciones
equivalentes.
4.1.5 Eliminación de Gauss y
Gauss-Jordan.
En matemáticas, la eliminación de Gauss-Jordan, llamada así debido a Carl Friedrich Gauss y Wilhelm Jordan, es un algoritmo del álgebra lineal para determinar las soluciones de un sistema de ecuaciones lineales, encontrar matrices e inversas. Un sistema de ecuaciones se resuelve por el método de Gauss cuando se obtienen sus soluciones mediante la reducción del sistema dado a otro equivalente en el que cada ecuación tiene una incógnita menos que la anterior. El método de Gauss transforma la matriz de coeficientes en una matriz triangular superior. El método de Gauss-Jordan continúa el proceso de transformación hasta obtener una matriz diagonal.
4.1.5.1 Definición de matriz.
En matemática, una matriz es un arreglo bidimensional de números. Dado que puede definirse tanto la suma como el producto de matrices, en mayor generalidad se dice que son elementos de un anillo. La notación de una matriz  tiene la forma:
tiene la forma:
 tiene la forma:
tiene la forma:
Las matrices se utilizan para múltiples aplicaciones y sirven, en particular, para representar los coeficientes de los sistemas de ecuaciones lineales o para representartransformaciones lineales dada una base. En este último caso, las matrices desempeñan el mismo papel que los datos de un vector para las aplicaciones lineales.
Pueden sumarse, multiplicarse y descomponerse de varias formas, lo que también las hace un concepto clave en el campo del álgebra lineal.
4.1.5.2 Expresión
matricial de un sistema de ecuaciones lineales.
4.1.5.3 Operaciones elementales sobre
renglones.
4.1.5.4 Reducción de Gauss y
Gauss-Jordan.
El Método de Gauss – Jordan o también llamado eliminación de Gauss – Jordan, es un método por el cual pueden resolverse sistemas de ecuaciones lineales con n números de variables, encontrar matrices y matrices inversas, en este caso desarrollaremos la primera aplicación mencionada.
Para resolver sistemas de ecuaciones lineales aplicando este método, se debe en primer lugar anotar los coeficientes de las variables del sistema de ecuaciones lineales en su notación matricial:
4.1.5.5 Sistemas homogéneos.
4.2 Álgebra de
Matrices.
Una matriz es un arreglo ordenado de números (llamados elementos o componentes)) distribuídos en m filas y n columnas ( matriz de orden m por n )
En general a las matrices se les designará por una letra mayúscula A, B, C, M etc..
4.2.1 Tipos de matrices (cuadrada,
rectangular, triangular, matriz identidad, matriz transpuesta).
4.2.2 Operaciones con matrices (suma,
diferencia, multiplicación por escalar y producto de matrices).
Suma de matrices
Dadas dos matrices de la misma dimensión, A=(aij) y B=(bij), se define la matriz suma como: A+B=(aij+bij).
La matriz suma se obtienen sumando los elementos de las dos matrices que ocupan la misma misma posición.
Producto de un escalar por una matriz
Dada una matriz A=(aij) y un número real k R, se define el producto de un número real por una matriz: a la matriz del mismo orden que A, en la que cada elemento está multiplicado por k.
R, se define el producto de un número real por una matriz: a la matriz del mismo orden que A, en la que cada elemento está multiplicado por k.
kA=(k aij)
4.2.3 Propiedades de las operaciones con
matrices.
Propiedades de la suma de matrices
Interna:
La suma de dos matrices de orden m x n es otra matriz dimensión m x n.
Asociativa:
A + (B + C) = (A + B) + C
Elemento neutro:
A + 0 = A
Donde O es la matriz nula de la misma dimensión que la matriz A.
Elemento opuesto:
A + (−A) = O
La matriz opuesta es aquella en que todos los elementos están cambiados de signo.
Conmutativa:
A + B = B + A
Propiedades
de un escalar por una matriz
a · (b · A) = (a · b) · A A  Mmxn, a, b
Mmxn, a, b 

a · (A + B) = a · A + a · BA,B  Mmxn , a
Mmxn , a 

(a + b) · A = a · A + b · A A  Mmxn , a, b
Mmxn , a, b 

1 · A = A A  Mmxn
Mmxn
4.2.4 Matriz
inversa.
Si premultiplicamos (multiplicamos por la izquierda) o posmultiplicamos (multiplicamos por la derecha) una matriz cuadrada por su inversa obtenemos la matriz identidad.
A · A−1 = A−1 · A = I
Propiedades
1 (A · B)−1 = B−1 · A−1
2 (A−1)−1 = A
3 (k · A)−1 = k−1 · A−1
4 (At)−1 = (A−1)t
4.3 Determinantes
4.3.1 Definición de un determinante.
En Matemáticas se define el determinante como una forma multilineal alternada de un cuerpo. Esta definición indica una serie de propiedades matemáticas y generaliza el concepto de determinante haciéndolo aplicable en numerosos campos. Sin embargo, el concepto de determinante o de volumen orientado fue introducido para estudiar el número de soluciones de los sistemas de ecuaciones lineales.
4.3.2 Expansión por cofactores.
4.3.3 Propiedades
de los determinantes.
1 |At|= |A|
El determinante de una matriz A y el de su traspuesta At son iguales.
2 |A| = 0 Si:
Posee dos filas (o columnas) iguales.
Todos los elementos de una fila (o una columna) son nulos.
Los elementos de una fila (o una columna) son combinación lineal de las otras.
F3 = F1 + F2
3 Un determinante triangular es igual al producto de los elementos de la diagonal principal.
4 Si en un determinante se cambian entre sí dos filas (o dos columnas), su valor sólo cambia de signo.
5 Si a los elementos de una fila (o una columna) se le suman los elementos de otra multiplicados previamente por un número real, el valor del determinante no varía.
Es decir, si una fila (o una columna) la transformamos en una combinación lineal de las demás, el valor del determinante no varía.
6 Si se multiplica un determinante por un número real, queda multiplicado por dicho número cualquier fila (o cualquier columna), pero sólo una.
7 Si todos los elementos de una fila (o columna) están formados por dos sumandos, dicho determinante se descompone en la suma de dos determinantes en los que las demás filas (o columnas) permanecen invariantes.
8 |A · B| =|A| · |B|
El determinante de un producto es igual al producto de los determinantes.
4.3.4 Regla de Cramer.
La regla de Cramer es un teorema del álgebra lineal que da la solución de un sistema lineal de ecuaciones en términos de determinantes. Recibe este nombre en honor aGabriel Cramer (1704 - 1752), quien publicó la regla en su Introduction à l'analyse des lignes courbes algébriques de 1750, aunque Colin Maclaurin también publicó el método en su Treatise of Geometry de 1748 (y probablemente sabía del método desde 1729).1
La regla de Cramer es de importancia teórica porque da una expresión explícita para la solución del sistema. Sin embargo, para sistemas de ecuaciones lineales de más de tres ecuaciones su aplicación para la resolución del mismo resulta excesivamente costosa: computacionalmente, es ineficiente para grandes matrices y por ello no es usado en aplicaciones prácticas que pueden implicar muchas ecuaciones. Sin embargo, como no es necesario pivotar matrices, es más eficiente que la eliminación gaussiana para matrices pequeñas, particularmente cuando son usadas operaciones SIMD.
Si 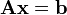 es un sistema de ecuaciones.
es un sistema de ecuaciones.  es la matriz de coeficientes del sistema,
es la matriz de coeficientes del sistema,  es el vector columna de las incógnitas y
es el vector columna de las incógnitas y  es el vector columna de los términos independientes. Entonces la solución al sistema se presenta así:
es el vector columna de los términos independientes. Entonces la solución al sistema se presenta así:
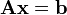 es un sistema de ecuaciones.
es un sistema de ecuaciones.  es la matriz de coeficientes del sistema,
es la matriz de coeficientes del sistema,  es el vector columna de las incógnitas y
es el vector columna de las incógnitas y  es el vector columna de los términos independientes. Entonces la solución al sistema se presenta así:
es el vector columna de los términos independientes. Entonces la solución al sistema se presenta así:
donde  es la matriz resultante de reemplazar la j-ésima columna de
es la matriz resultante de reemplazar la j-ésima columna de  por el vector columna
por el vector columna  . Hágase notar que para que el sistema sea compatible determinado, el determinante de la matriz
. Hágase notar que para que el sistema sea compatible determinado, el determinante de la matriz  ha de ser no nulo.
ha de ser no nulo.
 es la matriz resultante de reemplazar la j-ésima columna de
es la matriz resultante de reemplazar la j-ésima columna de  por el vector columna
por el vector columna  . Hágase notar que para que el sistema sea compatible determinado, el determinante de la matriz
. Hágase notar que para que el sistema sea compatible determinado, el determinante de la matriz  ha de ser no nulo.
ha de ser no nulo.
Sistema de 2x2
Para la resolución de un sistema de dos ecuaciones con dos incógnitas, de la forma. Dado el sistema de ecuaciones:
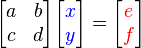
Se representa matricialmente :
Entonces,  e
e  pueden ser encontradas con la regla de Cramer, con una división de determinantes, de la siguiente manera:
pueden ser encontradas con la regla de Cramer, con una división de determinantes, de la siguiente manera:
 e
e  pueden ser encontradas con la regla de Cramer, con una división de determinantes, de la siguiente manera:
pueden ser encontradas con la regla de Cramer, con una división de determinantes, de la siguiente manera:
4.4
Aplicaciones: Modelo insumo-producto, análisis de ventas y comportamiento del
consumidor.
Jagdish C. Arya, Robin W. Lardner. (2009). Matemáticas aplicadas a la administración y a la economía. Quinta edición. México: Pearson
Resumen Unidad 4
Esta unidad para mi fue la que más me llamo la atención, aparte de que a mi las Matemáticas me parecen muy interesantes y entretenidas, en está unidad las matrices se me hacen muy interesantes por la metodología que tienen para resolverse es muy entretenida y lo que más me llamo la atención es que para mi carrera este tema es muy usado para almacenar datos.
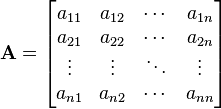

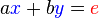
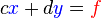

Me parece interesante que hayas incluido varios vídeos lo cuales hacen un buen conjunto de informacion para entender muy bien los temas
ResponderEliminarFelicidades.
Muy buen blog, la información es muy buena y aclara dudas con los videos que muestras
ResponderEliminareste blog esta muy bien hecho contiene buen información de todos los temas y muy buenos vídeos.
ResponderEliminarBuen trabajo Diego, buena información que se hace entendible para cada tema en especifico y en esta unidad 4 los videos que hay en tu blog facilitan la comprención de cada tema.
ResponderEliminarUn excelente trabajo, la manera en la que manejas el contenido permite que los temas se aprecien de una forma muy clara, el tema de Álgebra de Matrices es el que mas llamo mi atención, debido a que es uno de los temas que son mas difíciles de comprender gracias a las diferentes aplicaciones en las que se maneja dicho tema, pero la forma en la que tu lo manejas, permite que cualquier persona pueda asimilar la información de una manera rápida y coherente. Muchas felicidades.
ResponderEliminarMe parecio muy bien esta unidad con la información que pusiste y los videos se nos facilita entender más las matrices.
ResponderEliminarMuy buen blog, la informacion que proporcionas es muy buena, contiene muy buenos videos y ejemplos.
ResponderEliminarMe parce muy buen trabajo, sobre todo los vídeos que siempre ayudan más a la comprensión de las matemáticas,haces muy buenas explicaciones de todos los temas.
ResponderEliminarmuy buen trabajo.
Muy buen blog, se comprende muy bien el tema y los videos muy claros se nota la dedicacion y el desempeño que expresastes en el, excelente trabajo!
ResponderEliminarme gusto mucho tu blog diego, tienes la información bien organizada y es muy clara tus videos son muy buenos.
ResponderEliminarDiego muy buen trabajo, en tu blog, lo que más me llamó la atención es que cada tipo de matrices la definiste de una manera muy clara y detallada ya que aparece el procedimiento para solucionar cada tipo de matrices como lo vimos durante el curso; y aparte de eso toda la información muy organizada y los videos muy acertados para la explicación de los temas.
ResponderEliminarMuy buen blog Diego.
Felicidades.
Diego, no esperaba menos de tu parte compañero, tan buen trabajo como esperaba, todo muy bien detallado y hasta con iformación extra como pilón jejejeje por ejemplo en los tipos de matrices me pusiste hasta para llevar xD genial tu blog y seguro que puedes explicarme todos los temas tan bien como los autores jejeje. Excelente trabajo!
ResponderEliminarMuy buen trabajo, la información esta muy completo y otra cosa de la que me di cuenta es muy bueno poner el derecho de autor ya que si tu quieres investigar algo no se te dificulte.
ResponderEliminarFelicidades Diego.!
ResponderEliminarEl que haya incluido varios videos me agrado mucho, ya que sirven de apoyo para un mejor aprendizaje(:
Muy buena información y los videos complementan perfectamente para entender mejor. buen trabajo Diego
ResponderEliminarQue buen trabajo diego, me encato tu blog se nota tu dedicacion porque la informacion esta perfecta es de las mejores que e visto de verdad felicidades me encanto tu blog !
ResponderEliminarMuy buen blog buen trabajo e información, los videos hacen mas fácil la manera de entender la información. Me parece agradable que te tomaras el tiempo de desglosar los temas y dedicarle tiempo para ayudar a otros.
ResponderEliminarMuy buen trabajo Diego muy buena información y muy completa felicidades por tu trabajo
ResponderEliminarMuy buen trabajo diego, esta muy completa tu informacion
ResponderEliminarexcelente trabajo diego
ResponderEliminartu informacion es muy buena y entendible
felicidades