Objetivo Particular del Periodo:
El alumno
comprenderá los conceptos básicos del cálculo diferencial en varias variables,
así como la resolución de problemas en el entorno económico-administrativo,
enfatizando aquellos del área de optimización de recursos.
1.1 Funciones en dos variables.
Una función de dos variables es una regla de correspondencia que asigna a cada pareja de números reales (x, y) un y sólo un número real z.
El conjunto de parejas ordenadas para las cuales la regla de correspondencia dá un número real se llama dominio de la función. El conjunto de valores z que corresponden a los pares ordenados se llama imagen o contradominio.
Una función de dos variables se denota usualmente con la notación
z = f (x, y)
Las variables x, y se llaman variables independientes, y z se llama variable dependiente.
La gráfica de una función de dos variables es el conjunto de puntos con coordenadas (x, y, z) en donde (x, y) está en el dominio de f y z = f (x, y).
Este conjunto de puntos forma una superficie en el espacio tridimensional.


En consecuencia, la grafica de una función f de dos variables es una superficie que consta de todos los puntos del espacio tridimensional cuyas coordenadas cartesianas están determinadas por las ternas ordenadas de números reales (x, y, z). Como el dominio de f es un conjunto de puntos del plano x, y, y puesto que cada par ordenado (x, y) del dominio de f corresponde a solo un valor de z, ninguna recta perpendicular al plano x,y puede intersectar a la grafica de f en mas de un punto.http://www.monografias.com/trabajos78/funciones-dominio-rango-curva-nivel/funciones-dominio-rango-curva-nivel.shtml
1.2 Derivadas parciales.
En matemática, una derivada parcial de una función de diversas variables, es su derivada respecto a una de esas variables manteniendo las otras como constantes. Las derivadas parciales son útiles en cálculo vectorial y geometría diferencial.
La derivada parcial de una función f respecto a la variable x se representa con cualquiera de las siguientes notaciones equivalentes:
Donde  es la letra 'd' redondeada, conocida como la 'd de Jacobi'.
es la letra 'd' redondeada, conocida como la 'd de Jacobi'.
 es la letra 'd' redondeada, conocida como la 'd de Jacobi'.
es la letra 'd' redondeada, conocida como la 'd de Jacobi'.
Cuando una magnitud  es función de diversas variables (
es función de diversas variables ( ,
, ,
, ,
,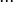 ), es decir:
), es decir:
 es función de diversas variables (
es función de diversas variables ( ,
, ,
, ,
,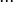 ), es decir:
), es decir:
Al realizar esta derivada obtenemos la expresión que nos permite obtener la pendiente de la recta tangente a dicha función  en un punto dado. Esta recta es paralela al plano formado por el eje de la incógnita respecto a la cual se ha hecho la derivada y el eje z.
en un punto dado. Esta recta es paralela al plano formado por el eje de la incógnita respecto a la cual se ha hecho la derivada y el eje z.
 en un punto dado. Esta recta es paralela al plano formado por el eje de la incógnita respecto a la cual se ha hecho la derivada y el eje z.
en un punto dado. Esta recta es paralela al plano formado por el eje de la incógnita respecto a la cual se ha hecho la derivada y el eje z.
Analíticamente el gradiente de una función es la máxima pendiente de dicha función en la dirección que se elija. Mientras visto desde el álgebra lineal, la dirección del gradiente nos indica hacia donde hay mayor variación en la función. https://es.wikipedia.org/wiki/Derivada_parcial
Weisstein, Eric W.. (2014 ). Derivada parcial. 18 de noviembre del 2015, de wikipedia.org Sitio web: https://es.wikipedia.org/wiki/Derivada_parcial
Weisstein, Eric W.. (2014 ). Derivada parcial. 18 de noviembre del 2015, de wikipedia.org Sitio web: https://es.wikipedia.org/wiki/Derivada_parcial
1.3 Máximos y mínimos de funciones de dos variables.
Si f está una función de x y y, entonces f tiene un máximo relativo a (a, b) si f(a, b) ³ f(x, y) para toda (x, y) en una pequeña cercanía de (a, b). Un mínimo relativo se define en manera parecida. f tiene un punto de silla en (a, b) si f tiene allí un mínimo relativo a lo largo de un corte y un máximo relativo a lo largo de un otro corte.
La función que se ilustra mas abajo tiene un mínimo relativo a (0, 0), un máximo relativo a (1, 1), y puntos de silla a (1, 0) y (0, 1).
En los casos que estudiamos, todos extremos relativos y puntos de silla que no sean en la frontera del dominio de f se ocurren a puntos críticos, que son las soluciones de las ecuaciones
- fx(x,y) = 0
y
- fy(x,y) = 0.
Prueba de segunda derivada para funciones de dos variables
Si f(x, y) está una función de dos variables, y (a, b) es un punto crítico de f. (Esto es, fx(a, b) = 0 y fy(a, b) = 0.) Suponga también que existen y son iguales las derivadas del segundo orden, de modo que, por teoremas de cálculo,fxy es igual a fyx. Sea
Si f(x, y) está una función de dos variables, y (a, b) es un punto crítico de f. (Esto es, fx(a, b) = 0 y fy(a, b) = 0.) Suponga también que existen y son iguales las derivadas del segundo orden, de modo que, por teoremas de cálculo,fxy es igual a fyx. Sea
- H = fxx(a, b)fyy(a, b) -[fxy(a, b)]2.
Entonces
- f tiene un mínimo relativo a (a, b) si H > 0 y fxx(a,b) > 0,
f tiene un máximo relativo a (a, b) si H > 0 y fxx(a,b) < 0, y
f tiene un punto de silla a (a, b) si H < 0.
Si H = 0 la prueba no dice nada, entonces necesitamos analizar la gráfica para buscar más información.
1.4 Aplicaciones: Optimización de funciones de dos variables que representen gastos, ingresos o utilidad.
Los metodos para hallar valores extremos que hemos aprendido tienen aplicaciones practicas en muchas areas de nuestra vida. Una persona de negocios quiere minimizar los costos y maximizar las utilidaddes. El principio de Fermat, en optica, afirma que la luz sigue la trayectoria que recorre en el menor tiempo. Lo que en algunos casos se conoce como la linea recta. En esta sección trataremos de resolver problemas como lo de maximizar áreas, volúmenes y utilidades, minimizar distancias, tiempos y costos.
En la solucion de problemas practicos, el desafio mas grande suele ser convertir el problema en palabras en una problema matematico de optimazion, establecer la funcion que debe maximizarse o minimizarse. Reucerdo los principios de soluciòn de problemas.
Pasos para la solucion de problemas de optimizacion
- COMPRENDA EL PROBLEMA: El primer paso, es leer el problema con cuidado hasta que se entienda con claridad. Hagase preguntas como: Cual es la incognita?, ¿Cuáles son las cantidades dadas?, ¿Cuáles son las condiciones dadas?.
- DIBUJE UN DIAGRAMA DEL PROBLEMA: En la mayor parte de los problemas, resulta util dibujar un diagrama e identificar en el las cantidades dadas requeridas.
- INTRODUZCA NOTACION: Asigne un simbolo a la cantidad que se va a maximizar o minimizar. Por ejemplo V = volumen, h = altura, b = base etc.
- Escriba una fórmula para la función objetivo Q que se maximizará o minimizará, en términos de las variables.
- Utilice las condiciones del problema para eliminar todas, excepto una de esta variables, y por consiguiente expresar Q como una función de una sola variable.
- DERIVAR
- IGUALAR LA DERIVADA: A cero para encontrar los puntos criticos.
- SEGUNDA DERIVADA: Deducir con la prueba de la segunda derivada si los puntos criticos son máximos ó mínimos.
- DAR LA SOLUCION: Recuerda dar una solucion clara de su problema en notacion Ingenieril.
Otra Forma de verlo
- . Se plantea la función que hay que maximizar o minimizar.
- . Se plantea una ecuación que relacione las distintas variables del problema, en el caso de que haya más de una variable.
- .Se despeja una variable de la ecuación y se sustituye en la función de modo que nos quede una sola variable.
- . Se deriva la función y se iguala a cero, para hallar los extremos locales.
- . Se realiza la 2ª derivada para comprobar el resultado obtenido.
Jagdish C. Arya, Robin W. Lardner. (2009). Matemáticas aplicadas a la administración y a la economía. Quinta edición. México: Pearson
Resumen Unidad 1
En esta unidad vimos lo que son las funciones con dos o más variables pero lo que en verdad me llamo más la atención de esta unidad fueron las derivadas parciales, ya que en este tema me agrado mucho poder sacar más de una derivada y la manera en que van los pasos a seguir para sacarlas con respecto a "x" y "y", tomando en cuenta la letra que no estas derivando respecto a ella, eso para mi fue lo más entretenido por mi gusto de esta materia.

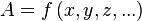
No hay comentarios:
Publicar un comentario