miércoles, 18 de noviembre de 2015

Unidad 2: Integración

Objetivo Particular del Periodo:
El alumno entenderá el concepto de integral y su relación con la derivada. Resolverá problemas de aplicación dando énfasis a aquellos relacionados con las áreas económico-administrativas tales como: Economía, Mercadotecnia, Administración, Turismo, Recursos Humanos, Sistemas de Información y Negocios Internacionales.

 2.1 Antiderivada. 

La antiderivada es la función que resulta del proceso inverso de la derivación, es decir, consiste en encontrar una función que, al ser derivada produce la función dada.
Por ejemplo:
Si f(x) = 3×2, entonces, F(x) = x3, es una antiderivada de f(x). Observe que no existe una derivada única para cada función. Por ejemplo, si G(x) = x3+ 5, entonces es otra antiderivada de f(x).
La antiderivada también se conoce como la primitiva o la integral indefinida se expresa de la siguiente manera: en donde: f(x) es el integrando; dx, la variable de integración o diferencial de x y C es la constante de integración.



2.2 Integral indefinida. 

Integral indefinida es el conjunto de las infinitas primitivas que puede tener una función.
Se representa por ∫ f(x) dx.
Se lee como "la integral indefinida de f(x) respecto a x" Por lo tanto, f(x) dx es una conjunto de funciones; no es una función sola, ni un número.
La función f que se está integrando se llama el integrando, y la variable x se llama la variable de integración.
C es la constante de integración y puede tomar cualquier valor numérico real.
Si F(x) es una primitiva de f(x) se tiene que:
∫ f(x) dx = F(x) + C
Para comprobar que la primitiva de una función es correcta basta con derivar.


2.2.1 Integración con condiciones iniciales. 

En cálculo, la integral indefinida de una función dada (es decir, el conjunto de todas las primitivas de la función) se escribe siempre con una constante, la constante de integración.1 2 Esta constante expresa una ambigüedad inherente a la construcción de primitivas. Si una función f está definida en un intervalo y F es una primitiva de f, entonces el conjunto de todas las primitivas de f viene dado por las funciones F (x) + C, siendo C, una constante arbitraria.
https://es.wikipedia.org/wiki/Constante_de_integraci%C3%B3n
Stewart, James. (2008). Constante de integración. 18 de noviembre del 2015, de Calculus: Early Transcendentals (6ª edición) Sitio web: https://es.wikipedia.org/wiki/Constante_de_integraci%C3%B3n




2.3 Fórmulas básicas de integración. 



2.3.1 Integral indefinida de una constante. 

La integral de una constante es igual a la constante por x.
integral de una constante

Ejemplo

integral de una constante

Integral de cero

integral de cero




2.3.2 Integral de una constante por una variable. 



2.3.3 Integral de xn 




2.3.4 Integral de en 



2.3.5 Integral de una constante por una función de x. 



2.3.6 Integral de una suma (diferencia) de funciones. 



Dada una función f(x) y un intervalo [a,b], la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x = a y x = b.
gráfica
La integral definida se representa por símbolo integral definida.
∫ es el signo de integración.
a límite inferior de la integración.
b límite superior de la integración.
f(x) es el integrando o función a integrar.
dx es diferencial de x, e indica cuál es la variable de la función que se integra.

Propiedades de la integral definida

1. El valor de la integral definida cambia de signo si se permutan los límites de integración.
propiedad de la integral definida
2. Si los límites que integración coinciden, la integral definida vale cero.
propiedad
3. Si c es un punto interior del intervalo [a, b], la integral definida se descompone como una suma de dos integrales extendidas a los intervalos [a, c] y [c, b].
propiedad
4. La integral definida de una suma de funciones es igual a la suma de integrales·
propiedad
5. La integral del producto de una constante por una función es igual a la constante por la integral de la función.
propiedad

2.3.7 Regla de la potencia. 

 La  de la  de la integración te da la  general para la integral de cualquier variable elevada a cualquier potencia excepto -1, lo que representa un caso especial. Ya que las integrales son primitivas, en otras palabras, si integras la derivada de una función, terminas con la función original, piensa en la regla de la potencia de la integración como hacer lo contrario de lo que hace la regla de la potencia para los derivados.
  1. 1
    Convierte las raíces cuadradas, raíces de otras potencias y potencias en los denominadores a las funciones de potencia estándar. La raíz cuadrada de x es igual a x ^ (1/2), la raíz cúbica de x es igual a x ^ (1/3) y así sucesivamente para las otras raíces. Para mover una potencia del denominador al numerador, toma la inversa de la potencia: 1 / x ^ 2 = x ^ -2, por ejemplo.
  2. 2
    Agrega  al poder. Para int [(x ^ 3) dx], por ejemplo, x ^ 3 se convierte en x 
  3. Divide el resultado entre el nuevo poder. Por ejemplo, x ^ 4 se convierte en (x ^ 4) / 4
  4. http://www.ehowenespanol.com/utilizar-regla-potencia-integracion-calculo-como_129387/
  5. Lamar University. (2015). Cómo utilizar la regla de la potencia de la integración en cálculo. 18 de noviembre del 2015, de Paul Dawkins Sitio web: http://www.ehowenespanol.com/utilizar-regla-potencia-integracion-calculo-como_129387/



2.3.7.1 Integrales que incluyen un 



2.3.7.2 Integrales que incluyen funciones exponenciales. 

La siguiente es una lista de integrales de funciones exponenciales (Agrégese a cada integral una constante arbitraria).

\int e^{cx}\;dx = \frac{1}{c} e^{cx}
\int xe^{cx}\; dx = \frac{e^{cx}}{c^2}(cx-1)
\int x^2 e^{cx}\;dx = e^{cx}\left(\frac{x^2}{c}-\frac{2x}{c^2}+\frac{2}{c^3}\right)
\int x^n e^{cx}\; dx = \frac{1}{c} x^n e^{cx} - \frac{n}{c}\int x^{n-1} e^{cx} dx
\int\frac{e^{cx}\; dx}{x} = \ln|x| +\sum_{i=1}^\infty\frac{(cx)^i}{i\cdot i!}
\int\frac{e^{cx}\; dx}{x^n} = \frac{1}{n-1}\left(-\frac{e^{cx}}{x^{n-1}}+c\int\frac{e^{cx} dx}{x^{n-1}}\right) \qquad\mbox{(para }n\neq 1\mbox{)}
\int e^{cx}\ln x\; dx = \frac{1}{c}\left(e^{cx}\ln|x|-\int\frac{e^{cx} dx}{x}\right)
\int e^{cx}\sin bx\; dx = \frac{e^{cx}}{c^2+b^2}(c\sin bx - b\cos bx)
\int e^{cx}\cos bx\; dx = \frac{e^{cx}}{c^2+b^2}(c\cos bx + b\sin bx)
\int e^{cx}\sin^n x\; dx = \frac{e^{cx}\sin^{n-1} x}{c^2+n^2}(c\sin x-n\cos x)+\frac{n(n-1)}{c^2+n^2}\int e^{cx}\sin^{n-2} x\;dx
\int e^{cx}\cos^n x\; dx = \frac{e^{cx}\cos^{n-1} x}{c^2+n^2}(c\cos x+n\sin x)+\frac{n(n-1)}{c^2+n^2}\int e^{cx}\cos^{n-2} x\;dx
\int {1 \over \sigma\sqrt{2\pi} }\,e^{-{(x-\mu )^2 / 2\sigma^2}}\; dx= \frac{1}{2 \sigma} \left(1 + \mbox{erf}\,\frac{x-\mu}{\sigma \sqrt(2)}\right)
\int_{-\infty}^{\infty} e^{-\alpha x^2}dx = \sqrt{\frac{\pi}{\alpha}} = I(\alpha)
\int_{-\infty}^{\infty}x^{2n} e^{-\alpha x^2}dx = (-1)^n \frac{d^n}{d\alpha^n} \ I(\alpha) \ \xrightarrow {\mbox{si n = 1}} \ =\frac{\sqrt\pi}{2\alpha^{3/2}}





2.3.8 Integrales que incluyen funciones logarítmicas. 

\int\ln x\,dx = x\ln x - x
\int (\ln x)^2\; dx = x(\ln x)^2 - 2x\ln x + 2 x
\int (\ln x)^n\; dx = x(\ln x)^n - n\int (\ln x)^{n-1} dx \qquad\mbox{(para }n\neq 1\mbox{)}
\int \frac{dx}{\ln x} = \ln|\ln x| + \ln x + \sum^\infty_{i=2}\frac{(\ln x)^i}{i\cdot i!}
\int \frac{dx}{(\ln x)^n} = -\frac{x}{(n-1)(\ln x)^{n-1}} + \frac{1}{n-1}\int\frac{dx}{(\ln x)^{n-1}} \qquad\mbox{(para }n\neq 1\mbox{)}
\int x^m\ln x\;dx = x^{m+1}\left(\frac{\ln x}{m+1}-\frac{1}{(m+1)^2}\right) \qquad\mbox{(para }m\neq 1\mbox{)}
\int x^m (\ln x)^n\; dx = \frac{x^{m+1}(\ln x)^n}{m+1} - \frac{n}{m+1}\int x^m (\ln x)^{n-1} dx \qquad\mbox{(para }m,n\neq 1\mbox{)}
\int \frac{(\ln x)^n\; dx}{x} = \frac{(\ln x)^{n+1}}{n+1} \qquad\mbox{(para }n\neq 1\mbox{)}
\int \frac{\ln x\,dx}{x^m} = -\frac{\ln x}{(m-1)x^{m-1}}-\frac{1}{(m-1)^2 x^{m-1}} \qquad\mbox{(para }m\neq 1\mbox{)}
\int \frac{(\ln x)^n\; dx}{x^m} = -\frac{(\ln x)^n}{(m-1)x^{m-1}} + \frac{n}{m-1}\int\frac{(\ln x)^{n-1} dx}{x^m} \qquad\mbox{(para }m,n\neq 1\mbox{)}
\int \frac{x^m\; dx}{(\ln x)^n} = -\frac{x^{m+1}}{(n-1)(\ln x)^{n-1}} + \frac{m+1}{n-1}\int\frac{x^m dx}{(\ln x)^{n-1}} \qquad\mbox{(para }n\neq 1\mbox{)}
\int \frac{dx}{x\ln x} = \ln|\ln x|
\int \frac{dx}{x^n\ln x} = \ln|\ln x| + \sum^\infty_{i=1} (-1)^i\frac{(n-1)^i(\ln x)^i}{i\cdot i!}
\int \frac{dx}{x (\ln x)^n} = -\frac{1}{(n-1)(\ln x)^{n-1}} \qquad\mbox{(para }n\neq 1\mbox{)}
\int \sin (\ln x)\;dx = \frac{x}{2}(\sin (\ln x) - \cos (\ln x))
\int \cos (\ln x)\;dx = \frac{x}{2}(\sin (\ln x) + \cos (\ln x))



2.3.9 Integrales que incluyen (1/u)du 




2.3.10 Integrales incluyen au          



2.3.11 Integral por partes. 

El método de integración por partes permite calcular la integral de un producto de dos funciones aplicando lafórmula:
fórmula de la integral por partes
Las funciones logarítmicas, "arcos" y polinómicas se eligen como u.
Las funciones exponenciales y trígonométricas del tipo seno y coseno, se eligen como v'.

Caso 1

En este primer caso aplicamos la fórmula directamente, tomando la x como u.
integral
derivar
integrar
solución

Caso 2

Si al integrar por partes tenemos un polinomio de grado n, lo tomamos como u y se repite el proceso n veces.
integral
derivar
integrar
integral
derivar
integrar
integral
operaciones
derivar
integrar
integral
solución

2.4 Aplicaciones: Determinación de funciones de costo, utilidades, consumo, y ahorro a partir de sus marginales.



Jagdish C. Arya, Robin W. Lardner. (2009). Matemáticas aplicadas a la administración y a la economía. Quinta edición. México: Pearson

 Resumen Unidad 2
En esta unidad vimos distintas maneras de integración y pienso que esto es muy interesante ya que podemos observar que puede haber integraciones que no se pueden resolver por un método, entonces probamos con otro, claro que esto lleva un proceso desde el método más sencillo hasta el método más tedioso y extenso.

Publicado por en

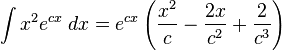
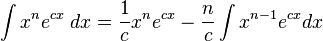
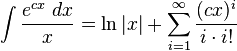
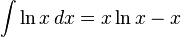
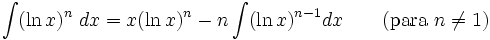
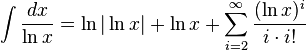
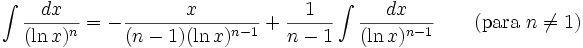
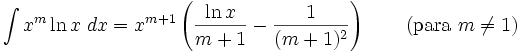
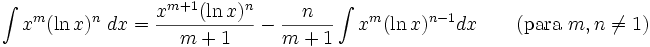
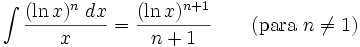
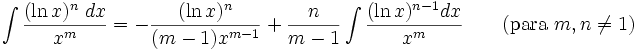
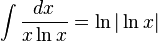
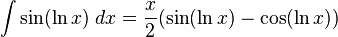
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)